Mehr Information
Hauptautor
Wicher, Jerzy
Co-Autoren
-
Medientyp
PDF-Dokument
Publikationsart
Tagungsbericht
Erscheinungsjahr
-
Verlag
EVU-Annual meeting 2007
Literaturstelle
Wicher, J: Influence of the second order partial derivatives in total differential method
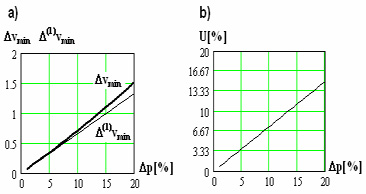
a) Veränderung Δv min, b) prozentuale Differenzen
Die Inputparameter von den bei Unfallrekonstruktionen angewendeten mathematischen Modellen sind selten genau bekannt. Dies bedeutet, dass die Berechnungsergebnisse auch mit einem gewissen Grad von Unsicherheit belastet sind, was mithilfe der Totaldifferenzialmethode eingeschätzt werden kann. Die üblicherweise angewendete Formel enthält nur Elemente der Taylor Erweiterung erster Ordnung. Immerhin wenn die Partialableitungen höherer Ordnung in Bezug auf die Parameter vorhanden sind und die Unsicherheit groß ist, kann damit gerechnet werden, dass der vernachlässigte Rest der Taylor Erweiterung signifikant sein kann. Die Analyse dieses Problems ist Gegenstand dieses Beitrags. Es wird gezeigt, dass die Verwendung der Totaldifferentialformel mit Elementen zweiter Ordnung der Taylor Reihen bei Parameterunsicherheit über 10 % berechtigt und empfehlenswert.
Dieser Artikel ist als PDF nur in englischer Sprache verfügbar.